- Network Sites:
-
 EEPower Day is a free 1-day virtual conference. Learn More
EEPower Day is a free 1-day virtual conference. Learn More
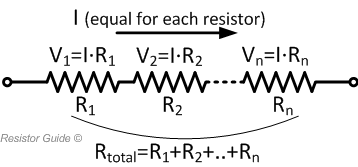
In many electrical circuits, resistors are connected in series or parallel. A designer might, for example, combine several resistors with standard values (E-series) to reach a specific resistance value. For series connection, the current through each resistor is equal. There is only one path for the current to follow. The voltage drop, however, is proportional to the resistance of each individual resistor. The equivalent resistance of several resistors in series is given by:
$$R_{eq} = \sum_{i=1}^n R_i = R_1 + R_2 + \dots + R_n$$
The voltage across each resistor is calculated with Ohm's law:
$$V_i = I · R_i$$
Consider a circuit as shown in the picture below. Two resistors R1 and R2 connected in series are subject to a constant current, I, of 5 A. How can we calculate the voltage drop for each resistor, and how can we determine the equivalent resistance value for the two resistors?
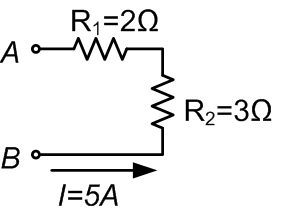
The current through each resistor is equal (5 A). Knowing this, and using Ohm's law, we can calculate the voltage drop for R1 and R2:
$$V_{resistor1} = I · R_1 = 5 · 2 = 10 V$$
$$V_{resistor2} = I · R_2 = 5 · 3 = 15 V$$
$$V_{eq} = V_{resistor1} + V_{resistor2} = 10 + 15 = 25 V$$
The equivalent resistance is equal to the sum of R1 and R2:
$$R_{eq} = R_1 + R_2 = 2 + 3 = 5 \Omega$$
This corresponds with the voltage drops that we calculated:
$$V_{eq} = I · R_{eq} = 5 · 5 = 25 V$$
Take a look at the article discussing resistors in parallel to find practical examples of how to solve a resistor network with resistors that are connected in both series and parallel. The following video also provides additional information on calculating the equivalent resistance of resistor networks.